fupermod: Functional Performance Models of heterogeneous processors

Classes | Typedefs | Functions

Data partitioning

Classes

struct  fupermod_part
struct  fupermod_dist
struct  fupermod_partitioner

Typedefs

typedef int(* fupermod_partition )(fupermod_dist *dist, int size, fupermod_model **models)

Functions

fupermod_dist * fupermod_dist_alloc (long long int D, int size)
void fupermod_dist_free (fupermod_dist *dist)
int fupermod_dist_read (FILE *stream, fupermod_dist *dist, fupermod_process_conf *confs, int maxsize)
int fupermod_dist_write (FILE *stream, fupermod_dist *dist, fupermod_library *library, fupermod_process_conf *confs)
long long int fupermod_dist_total (fupermod_dist *dist)
int fupermod_dist_test_total (fupermod_dist *dist)
int fupermod_dist_test_times (fupermod_point *points, int size, double eps)
int fupermod_dist_scatter (fupermod_dist *dist, long long int *d, int root, MPI_Comm comm)
int fupermod_partition_homogeneous (fupermod_dist *dist, int size, fupermod_model **models)
int fupermod_partition_basic (fupermod_dist *dist, int size, fupermod_model **models)
int fupermod_partition_geometric (fupermod_dist *dist, int size, fupermod_model **models)
int fupermod_partition_multiroot (fupermod_dist *dist, int size, fupermod_model **models)
fupermod_partitioner partitioner_switch (int algorithm, int smooth, int benchsize)

Typedef Documentation

typedef int(* fupermod_partition)(fupermod_dist *dist, int size, fupermod_model **models)

Partitioning algorithm. All partitioning algorithms must implement this interface.

Parameters:
dist optimal data distribution (input/output parameter)
size number of processors
models time functions

Function Documentation

fupermod_dist* fupermod_dist_alloc ( long long int  D,
int  size 
)

Allocates an equal distribution

void fupermod_dist_free ( fupermod_dist *  dist  ) 

Frees the distribution

int fupermod_dist_read ( FILE *  stream,
fupermod_dist *  dist,
fupermod_process_conf *  confs,
int  maxsize 
)

Reads distribution from file

Reads fupermod_dist from file

int fupermod_dist_write ( FILE *  stream,
fupermod_dist *  dist,
fupermod_library *  library,
fupermod_process_conf *  confs 
)

Writes distribution to file

Writes fupermod_part to file

long long int fupermod_dist_total ( fupermod_dist *  dist  ) 

Returns the total problem size

Parameters:
dist distribution
Returns:
total problem size
int fupermod_dist_test_total ( fupermod_dist *  dist  ) 

Tests the problem sizes in the distribution

Parameters:
dist distribution
Returns:
true if sum of the parts is equal to the total problem size
int fupermod_dist_test_times ( fupermod_point *  points,
int  size,
double  eps 
)

Tests the times in the distribution

Parameters:
points array of size size.
size number of proc.
eps maximum relative difference between times
Returns:
true if the relative difference between times is less than eps
int fupermod_dist_scatter ( fupermod_dist *  dist,
long long int *  d,
int  root,
MPI_Comm  comm 
)

Scatters the distribution

Parameters:
dist distribution (significant only at root)
d problem size
root root
comm MPI communicator
int fupermod_partition_homogeneous ( fupermod_dist *  dist,
int  size,
fupermod_model **  models 
)

Returns an homogeneous distribution (for experimental comparison)

int fupermod_partition_basic ( fupermod_dist *  dist,
int  size,
fupermod_model **  models 
)

Proportional data partitioning. Uses models of any type (with the constant models provided by fupermod_model_constant_alloc, this function will perform the traditional data partitioning algorithm)

int fupermod_partition_geometric ( fupermod_dist *  dist,
int  size,
fupermod_model **  models 
)

Geometrical data partitioning. Requires models providing the particular shape of the speed (for example, the piecewise model provided by fupermod_model_piecewise_alloc)

int fupermod_partition_multiroot ( fupermod_dist *  dist,
int  size,
fupermod_model **  models 
)

Finds the optimal partition. Solves a system of non-linear equations 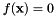$ f(\mathbf{x}) = 0 $, where 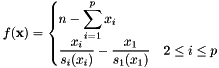$ f(\mathbf{x}) = \begin{cases} n - \displaystyle\sum\limits_{i=1}^{p}x_i &\\ \displaystyle\frac{x_i}{s_i(x_i)} - \displaystyle\frac{x_1}{s_1(x_1)} & 2 \le i \le p \end{cases} $ by the least squares minimization of the residual of the system. Uses the HYBRJ algorithm (a modified version of Powell's Hybrid method) implemented in GSL. The iterative solution starts with 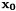$ \mathbf{x_0} $ given by the dist argument. dist is the resulting distribution.

fupermod_partitioner partitioner_switch ( int  algorithm,
int  smooth,
int  benchsize 
)

Sets up pointers to appropriate model and partition functions /param algorithm Number between 0 4. 0: Homogeneous distribution 1: Constant performance model 1 2: Constant performance model 2 3: Geometric algorithm FFPM 4: FPM multiroot solver