CPM: A software tool for Communication Performance Modelling
Classes | |
| struct | LMO_model |
Defines | |
| #define | LMO_C3(n) (n) * ((n) - 1) * ((n) - 2) / 6 |
| #define | LMO_IJK2INDEX(n, i, j, k) (2 * (n) - (i) - 1) * ((i) - 1) * (i) / 4 + (2 * (n) - (i) - (j) + 1) * ((j) - (i)) / 2 + (k) - (j) - 1 |
Functions | |
| LMO_model * | LMO_alloc (int n) |
| void | LMO_free (LMO_model *model) |
| void | LMO_read (FILE *stream, LMO_model **model) |
| void | LMO_write (FILE *stream, const LMO_model *model) |
| void | LMO_estimate (MPI_Comm comm, MPIB_precision precision, MPIB_msgset msgset, int parallel, LMO_model **model) |
| double | LMO_predict_p2p (void *_this, int i, int j, int M) |
| double | LMO_predict_scatter_flat (void *_this, int root, int M) |
| double | LMO_predict_gather_flat (void *_this, int root, int M) |
| void | HLMO_estimate (MPI_Comm comm, MPIB_precision precision, MPIB_msgset msgset, LMO_model **model) |
| double | HLMO_predict_p2p (void *_this, int i, int j, int m) |
| double | HLMO_predict_scatter_flat (void *_this, int root, int m, int n) |
Detailed Description
This module provides building of the LMO model and estimation of the execution time of point-to-point and collective communication operations.
Define Documentation
| #define LMO_C3 | ( | n | ) | (n) * ((n) - 1) * ((n) - 2) / 6 |
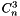
| #define LMO_IJK2INDEX | ( | n, | ||
| i, | ||||
| j, | ||||
| k | ||||
| ) | (2 * (n) - (i) - 1) * ((i) - 1) * (i) / 4 + (2 * (n) - (i) - (j) + 1) * ((j) - (i)) / 2 + (k) - (j) - 1 |
The index of the 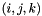 element in the array of
element in the array of 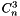 elements,
elements, 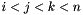 .
. 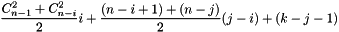 .
.
Function Documentation
| LMO_model* LMO_alloc | ( | int | n | ) |
Allocates the LMO model.
- Parameters:
-
n number of processors
- Returns:
- LMO model
| void LMO_free | ( | LMO_model * | model | ) |
Frees the LMO model.
- Parameters:
-
model LMO model
| void LMO_read | ( | FILE * | stream, | |
| LMO_model ** | model | |||
| ) |
Reads the LMO model.
| void LMO_write | ( | FILE * | stream, | |
| const LMO_model * | model | |||
| ) |
Writes the LMO model.
| void LMO_estimate | ( | MPI_Comm | comm, | |
| MPIB_precision | precision, | |||
| MPIB_msgset | msgset, | |||
| int | parallel, | |||
| LMO_model ** | model | |||
| ) |
Estimates the parameters of the LMO model.
- Measures one-to-many execution time for the message sizes
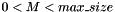 and performs the Bai & Perron algorithm over the F statistic for the data to find the
and performs the Bai & Perron algorithm over the F statistic for the data to find the  breakpoint in the piecewise linear regression
breakpoint in the piecewise linear regression  ~
~ 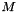 .
. - Measures many-to-one execution time for the message sizes
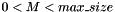 and performs the Bai & Perron algorithm over the F statistic for the data to find the
and performs the Bai & Perron algorithm over the F statistic for the data to find the 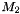 breakpoint in the piecewise linear regression
breakpoint in the piecewise linear regression 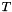 ~
~ 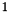 .
. - In the loop, measures many-to-one execution time for the message sizes
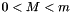 with the stride reduced twice each time.
with the stride reduced twice each time. 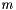 is a message size for which a tenfold escalation of the execution time has been observed at the previous step. As the stride reaches 1 byte,
is a message size for which a tenfold escalation of the execution time has been observed at the previous step. As the stride reaches 1 byte, 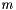 is truncated to a kb value, which will be
is truncated to a kb value, which will be 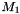 .
. - Finds the fixed processing delays and latencies.
For each 3 nodes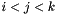 , measures execution times and solves systems of equations:
, measures execution times and solves systems of equations:
![$ \begin{cases} T_{ij}(0) = 2 (C_i + L_{ij} + C_j) & i \xlongleftrightarrow[0]{0} j \\ T_{jk}(0) = 2 (C_j + L_{jk} + C_k) & j \xlongleftrightarrow[0]{0} k \\ T_{ik}(0) = 2 (C_i + L_{ik} + C_k) & i \xlongleftrightarrow[0]{0} k \\ T_{ijk}(0) = 2 (2 C_i + \displaystyle\max_{x = j, k}(L_{ix} + C_x)) & i \xlongleftrightarrow[0]{0} jk \\ T_{jik}(0) = 2 (2 C_j + \displaystyle\max_{x = i, k}(L_{jx} + C_x)) & j \xlongleftrightarrow[0]{0} ik \\ T_{kij}(0) = 2 (2 C_k + \displaystyle\max_{x = i, j}(L_{kx} + C_x)) & k \xlongleftrightarrow[0]{0} ij \\ \end{cases} $](form_45.png)
averages solutions:
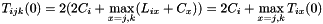
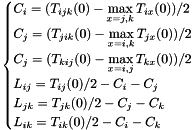
and checks confidence intervals. - Finds the variable processing delays and transmission rates.
For each 3 nodes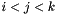 , solves systems of equations:
, solves systems of equations:
![$ \begin{cases} T_{ij}(M) = 2 (C_i + L_{ij} + C_j + M (t_i + \displaystyle\frac{1}{\beta_{ij}} + t_j)) & i \xlongleftrightarrow[M]{M} j \\ T_{jk}(M) = 2 (C_j + L_{jk} + C_k + M (t_j + \displaystyle\frac{1}{\beta_{jk}} + t_k)) & j \xlongleftrightarrow[M]{M} k \\ T_{ik}(M) = 2 (C_i + L_{ik} + C_k + M (t_i + \displaystyle\frac{1}{\beta_{ik}} + t_k)) & i \xlongleftrightarrow[M]{M} k \\ T_{ijk}(M) = 2 (2 C_i + M t_i) + \displaystyle\max_{x = j, k}(2 (L_{ix} + C_x) + M (\frac{1}{\beta_{ix}} + t_x)) & i \xlongleftrightarrow[0]{M} jk \\ T_{jik}(M) = 2 (2 C_j + M t_j) + \displaystyle\max_{x = i, k}(2 (L_{jx} + C_x) + M (\frac{1}{\beta_{jx}} + t_x)) & j \xlongleftrightarrow[0]{M} ik \\ T_{kij}(M) = 2 (2 C_k + M t_k) + \displaystyle\max_{x = i, j}(2 (L_{kx} + C_x) + M (\frac{1}{\beta_{kx}} + t_x)) & k \xlongleftrightarrow[0]{M} ij \\ \end{cases} $](form_48.png)
averages solutions:
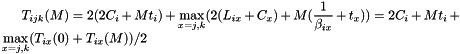
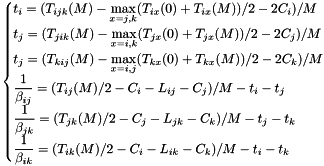
and checks confidence intervals.- Note:
- R must be initialized by LMO_init_R at root beforehand.
- Parameters:
-
comm communicator precision measurement precision msgset message set parallel several non-overlapped point-to-point communications at the same time if non-zero model LMO model (significant only at root)
| double LMO_predict_p2p | ( | void * | _this, | |
| int | i, | |||
| int | j, | |||
| int | M | |||
| ) |
Predicts the execution time of point-to-point communication. The execution time of 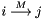 is equal to
is equal to
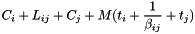
- Parameters:
-
_this LMO model i index of the processor j index of the processor M message size
- Returns:
- predicted execution time
| double LMO_predict_scatter_flat | ( | void * | _this, | |
| int | root, | |||
| int | M | |||
| ) |
Predicts the execution time of flat-tree scatter. 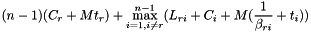
- Parameters:
-
_this LMO model root root processor M message size
- Returns:
- predicted execution time
| double LMO_predict_gather_flat | ( | void * | _this, | |
| int | root, | |||
| int | M | |||
| ) |
Predicts the execution time of flat-tree gather. 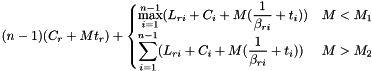
- Parameters:
-
_this LMO model root root processor M message size
- Returns:
- predicted execution time
| void HLMO_estimate | ( | MPI_Comm | comm, | |
| MPIB_precision | precision, | |||
| MPIB_msgset | msgset, | |||
| LMO_model ** | model | |||
| ) |
Estimates the parameters of the homogeneous LMO model (n = 2). Requires at least 3 processes. Based on the homogeneous LMO prediction of flat scatter 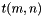 . Uses benchmarks for m = msgset.max_size and msgset.min_size, and n = comm_size and 0.9 * comm_size.
. Uses benchmarks for m = msgset.max_size and msgset.min_size, and n = comm_size and 0.9 * comm_size.
- See also:
- tests/hmodel.c
| double HLMO_predict_p2p | ( | void * | _this, | |
| int | i, | |||
| int | j, | |||
| int | m | |||
| ) |
Predicts the execution time of point-to-point communication, using the homogeneous LMO model
| double HLMO_predict_scatter_flat | ( | void * | _this, | |
| int | root, | |||
| int | m, | |||
| int | n | |||
| ) |
Predicts the execution time of flat-tree scatter, using the homogeneous LMO model


